مفهوم دنباله

مجموعه اعداد زوج طبیعی را در نظر بگیرید اولین عضو این مجموعه عدد ۲ است و n امین عضو آن ۲n است.
حال مجموعه اعداد طبیعی را در نظر بگیرید: 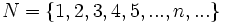با کمی دقت متوجه می‌شویم که می‌توان یک تابع یک به یک از مجموعه اعداد طبیعی به مجموعه اعداد طبیعی زوج تعریف نمود که در عضو از مجموعه اعداد طبیعی را به یک عضو از مجموعه اعداد طبیعی زوج متناظر کند.(مانند شکل)

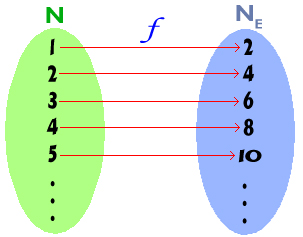
اگر این تناظر را به صورت مجموعه زوج های مرتب بنویسیم خواهیم داشت: 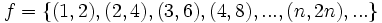متوجه می‌شویم تابع f از مجموعه اعداد طبیعی به مجموعه اعداد طبیعی زوج، تابعی است یک به یک که هر عضو از دامنه خود را دو برابر می‌کند و به یک عضو از مجموعه اعداد طبیعی زوج متناظر می‌کند و می‌توان چنین ضابطه‌ای برای آن تعیین نمود:
حال در مثالی دیگر تابع را در نظر بگیرید. بیاید بجای اینکه به جای متغیر تابع عددی حقیقی قرار دهیم، متغیرهای طبیعی را جایگزین کنیم. در این صورت داریم:

مشاهده می‌کنید این تابع نیز هر عدد طبیعی را به عنوان ورودی دریافت می‌کند و آن را به یک عدد دیگر نسبت می‌دهد با این تفاوت که این تابع دیگر یک به یک نمی‌باشد و فقط بین اعداد طبیعی و مجموعه اعداد حقیقی یک تناظر بوجود می‌آورد.
نمونه های دیگری نیز از این توابع وجود دارد مثلاً توابع ، ، که در آنها n عددی طبیعی است.
به چنین توابعی که از از مجموعه اعداد طبیعی به یک مجموعه دیگر تعریف می‌شوند دنباله می‌گوییم. در دنباله اعداد طبیعی زوج، عدد ۲ از برد تابع را جمله اول، عدد ۴ را جمله دوم و به همین ترتیب عدد ۲n را جمله n ام دنباله می‌گوییم. همین شیوه برای سایر دنباله‌ها نیز اعمال می‌شود.
در یک دنباله، اعداد طبیعی در دامنه به گونه‌ای به اعضای برد متناظر می‌شوند که عدد طبیعی متناظر شده بیانگر شماره آن جمله در برد باشد به عنوان مثال در دنباله اعداد طبیعی زوج، عدد ۱ در دامنه به عدد ۲ در برد که اولین جمله دنباله است متناظر می‌شود و عدد ۱۰ از دامنه به عدد ۲۰ از برد که جمله دهم است متناظر می‌شود و به همین ترتیب عدد n‌ در دامنه به عدد ۲n از برد که جمله n ام است متناظر می شود.

تعریف دنباله

دنباله (sequence) تابعی است که دامنه آن مجموعه اعداد طبیعی یا قطعه ای از مجموعه اعداد طبیعی باشد. پس در حالت کلی یک دنباله چون f تابعی است از مجموعه اعداد طبیعی به یک مجموعه دیگر چون A.

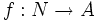
اگر دامنه دنباله قطعه ای از مجموعه اعداد طبیعی باشد دنباله را متناهی می‌گوییم و اگر دامنه دنباله خود مجموعه اعداد طبیعی باشد دنباله را نامتناهی می‌گوییم. به عنوان مثال دنباله اعداد طبیعی زوج کوچکتر از ۱۰ یک دنباله متناهی است چرا که دامنه آن قطعه ای از مجموعه اعداد طبیعی یعنی 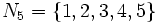است و دنباله اعداد زوج دنباله‌ای نامتناهی است چرا که دامنه آن خود مجموعه اعداد طبیعی است.

برای مشخص کردن یک دنباله مانند هر تابع دیگر باشد دامنه و ضابطه آن را مشخص کرد. ضابطه یک دنباله را در اصطلاح جمله عمومی آن دنباله می‌گوییم. اگر f یک دنباله باشد جمله عمومی آن را با (f(n و یا به صورتی معمول‌تر به صورت 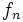نشان می‌دهیم. پس برای نمایش مقدار دنباله f به ازای عدد طبیعی n بجای نماد (f(n معمولا از نماد 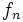استفاده می‌کنیم. به عنوان مثال در دنباله اعداد طبیعی زوج داریم:
برای نمایش خود دنباله از نماد استفاده می‌کنیم. پس دنباله اعداد طبیعی زوج را به این صورت نشان می دهیم:

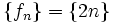
دنباله حقیقی

دنباله را دنباله حقیقی می‌گویند هرگاه تابعی از مجموعه اعداد طبیعی به مجموعه اعداد حقیقی باشد به عبارت دیگر تابعرا یک دنباله حقیقی می‌گویند.
به عنوان مثال دنبالهدنباله‌ای حقیقی است چرا که برد آن از مجموعه اعداد حقیقی است.

لازم به توضیح است معمولاً منظور از دنباله، دنباله حقیقی است.

نمودار یک دنباله

از آنجا که دنباله یک تابع با دامنه عداد طبیعی است می‌توان دنباله را بوسیله نمودار نیز نمایش داد. این نمایش با دو روش انجام می‌شود. در یک روش می‌توان مانند توابع دیگر آن را در دستگاه مختصات دکارتی رسم کرد و در روشی دیگر می‌توان جملات آن را به همراه ذکر شماره آن جمله روی محور اعداد نشان داد. با ذکر یک مثال دو روش را توضیح می‌دهیم. به عنوان مثال می‌خواهیم دنباله اعداد زوج را به هر دو روش نشان دهیم:

بوسیله رسم نمودار در دستگاه مختصات دکارتی: برای این منظور محور افقی را برای متغیر انتخاب کرده و محور عمودی را برای نمایش تغییرات جملات دنباله استفاده می‌کنیم. نمودار این دنباله به این صورت خواهد بود:

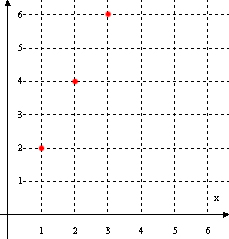
بوسیله رسم نمودار روی محور اعداد: برای این منظور روی محور اعداد مقدار جملات دنباله را یافته و شماره جمله را در بالا آن می‌نویسیم مانند این نمودار:

جمله عمومی یک دنباله

همانطور که گفته شد یک دنباله تابعی با دامنه مجموعه اعداد طبیعی است پس برای دنباله ها در حالت کلی می‌توان ضابطه تعیین کرد که به ضابطه یک دنباله جمله عمومی آن دنباله می‌گویند. جمله عمومی یک دنباله به منزله یک قانون است که بوسیله آن هر عضو از دامنه(مجموعه اعداد طبیعی) به یک عضو از مجموعه برد متناظر می‌شود و به ازای هر مقدار از متغیر n، جملات دنباله را تولید می‌کند.
به عنوان مثال جمله عمومی دنباله اعداد طبیعی زوج به صورت 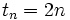است که همانند ضابطه تابع بوسیله آن می‌توان با قرار دادن هر n طبیعی جمله n ام 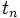را بدست آورد.
البته لازم به ذکر است همه دنباله‌ها دارای جمله عمومی نمی‌باشند. به عنوان مثال تا کنون جمله عمومی برای دنباله اعداد اول تعیین نشده است. همچنین ممکن است یک سری از اعداد را به عنوان جملات دنباله انتخاب نمود که نتوان میان آنها رابطه ای برقرار نمود و جمله عمومی برای آنها نوشت.
حال ممکن است این سوال پیش بیاید که آیا با در اختیار داشتن جملات یک دنباله می توان جمله عمومی آن را تعیین کرد؟
پاسخ را با یک مثال بررسی می‌کنیم. دنباله زیر را در نظر بگیرید:

می‌خواهیم جمله عمومی این دنباله را با توجه به جملاتش تعیین کنیم.
با مشاهده‌ی جملات ممکن است حدس شما این باشد که این دنباله، دنباله اعداد طبیعی فرد بزرگتر از یک است و جمله عمومی آن را می‌توان به این صورت نوشت:

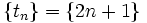
اما این ممکن است یک جمله عمومی برای این دنباله باشد. ممکن است جملات دنباله در ادامه به این روال پیش نروند
و جمله چهارم این دنباله عددی چون ۹ نباشد! چرا که ما از جمله سوم به بعد دنباله هیچ اطلاعی نداریم و هر عدد دیگری نیز می‌تواند باشد!
به عنوان مثال جمله عمومی دنباله فوق را می‌توان به این صورت نوشت:

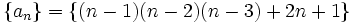
با نوشتن جملات این دنباله داریم:

مشاهده می‌کنید جملات این دنباله تا جمله سوم همانند دنباله است ولی از جمله سوم به بعد مانند آن دنباله عمل نمی کند.
پس همواره از روی جملات یک دنباله نمی‌توان جمله عمومی آن را به درستی تعیین کرد. اما معمولاً برای نوشتن جمله عمومی یک دنباله با توجه به جملات آن، ساده ترین حالت را در نظر می‌گیریم. لذا جمله عمومی 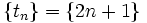برای این دنباله صحیح‌تر است و زودتر به ذهن خطور می‌کند.

رابطه بازگشتی و دنباله بازگشتی

به دنباله اعداد زوج دقت کنید: …,۲,۴,۶,۸,۱۰,۱۲
با کمی دقت در می‌یابید که برای بدست آوردن هر جمله کافی است جمله قبل را با عدد دو جمع کنید. به عنوان مثال برای بدست آوردن جمله پنجم(۱۰) کافی است جمله چهارم(۸) را با عدد دو جمع کنید. به این رابطه که بین جملات این دنباله برقرار است رابطه بازگشتی می گوییم.

تعریف: در بسیاری از دنباله‌ها بین هر جمله و جملات ماقبل یک رابطه‌ای وجود دارد که بوسیله آن می‌توان جملات بعدی را تعیین نمود. به چنین رابطه‌ای، رابطه بازگشتی می‌گوییم و به دنباله‌هایی با این رابطه، دنباله بازگشتی می‌گوییم.

از معروف ترین این دنباله ها می توان به دنباله فیبوناتچی و دنباله لوکا اشاره کرد.
به عنوان مثال دنباله فیبوناتچی دارای چنین رابطه‌ای است که بوسیله آن مشخص می‌شود:

که جملات آن به این صورت است: …,۱,۱,۲,۳,۵,۸,۱۳,۲۱
مشاهده می‌شود برای بدست آوردن هر جمله از جمله دوم به بعد کافی است دو جمله ماقبل آن جمله را با هم جمع کنیم. مثلا برای محاسبه جمله نهم داریم: