مقدمه
خط حقیقی: برای نمایش اعداد حقیقی از یک دستگاه مختصات بنام خط حقیقی یا محور x استفاده میکنیم. عدد حقیقی نظیر یک نقطه روی خط حقیقی مختص آن نقطه نامیده میشود. همان طور که میدانیم نقطهای از خط حقیقی که نظیر صفر است مبدأ نامیده میشود و اعدادی که در سمت راست مبدأ واقع میشوند طبق قرارداد اعداد مثبت و اعدادی که در سمت چپ مبدأ قرار دارند به عنوان اعداد منفی معرفی شدهاند. هر نقطه روی خط حقیقی نظیر یک و تنها یک عدد حقیقی است. این نوع رابطه را تناظر یک به یک مینامند.
صفحه دکارتی
همانطور که اعداد حقیقی را میتوان با نقاط روی خط حقیقی نشان داد، جفتهای مرتب اعداد حقیقی را میتوان با نقاط روی یک صفحه نمایش داد. جفت مرتب (x,y) از اعداد حقیقی دارای عضو اول x و عضو دوم y است. مدل نمایش جفتهای مرتب را دستگاه مختصات قائم یا صفحه دکارتی مینامند. این مدل عبارت است از دو خط حقیقی که در زوایای قائم متقاطع میباشند. خط حقیقی افقی را معمولا محور x و خط حقیقی قائم را محور y مینامند. نقطه اشتراکشان مبدأ نام دارد. همانطور که گفتیم صفحه مختصات دکارتی از متقاطع شدن دو محور حقیقی با یکدیگر در نقطهای به نام مبدأ حاصل میگردد. این تقاطع صفحه را به دو قسمت تقسیم میکند که به هر یک از این قسمتها یک ربع گفته میشود. بنابراین توسط دستگاه مختصات دکارتی ما میتوانیم یک صفحه را به چهار ربع تقسیم کنیم.
مختصات یک نقطه
در صفحه دکارتی نقاط از دو مؤلفه به نامهای x , y تشکیل یافتهاند که با یکدیگر تشکیل جفتهای مرتب را میدهند مانند (x و y) در واقع جفتهای مرتب (x و y) مختصات یک نقطه در صفحه دکارتی میباشند. عدد x فاصله جهت دار از محور y تا نقطه و y فاصله جهت دار از محور x تا نقطه میباشند.
فرمولهای فاصله و نقطه میانی در صفحه دکارتی
فاصله: برای بدست آوردن فاصله بین دو نقطه
Latex Error:
{x_1,y_1}
و
Latex Error:
{x_2,y_2}
قضیه فیثاغورس را به یاد میآوریم که در یک مثلث قائم الزاویه به وتر و اضلاع a و b داریم: 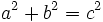 و همین طور عکس قضیه نیز برقرار است. بنابراین برای بدست آوردن فاصله d بین دو نقطه مذکور میتوانیم توسط این دو نقطه مثلث قائم الزاویهای تشکیل دهیم طول ضلع قائم این مثلث توسط رابطه
و همین طور عکس قضیه نیز برقرار است. بنابراین برای بدست آوردن فاصله d بین دو نقطه مذکور میتوانیم توسط این دو نقطه مثلث قائم الزاویهای تشکیل دهیم طول ضلع قائم این مثلث توسط رابطه
Latex Error:
{|y_2-y_1|}
و طول ضلع افقی توسط رابطه
Latex Error:
{|x_2-x_1|}
بدست میآید. طبق قضیه فیثاغورث توان دوم فاصله با مجموع مربع دو ضلع دیگر مساوی است.
بنابراین
Latex Error:
{d=\sqr {(x_2-x_1)
۲}}
فرمول نقطه میانی: نقطه میانی پاره خط واصل بین نقاط
Latex Error:
{x_1,y_1}
و
Latex Error:
{x_2,y_2}
عبارت است از:
Latex Error:
{( \frac {x_1+x_2}{2} , \frac {y_1+y_2}{2})}
تعریف دایره در صفحه دکارتی: فرض کنیم (k و h) نقطهای در صفحه بوده و r>0. مجموعه تمام نقاط (x,y) که r فاصله بین (k و h) و (x و y) باشد یک دایره نام دارد. نقطه (k و h) را مرکز و r را شعاع دایره مینامیم. از فرمول فاصله میتوان برای نوشتن معادله دایره استفاده کنیم.
مفهوم نمودار در یک صفحه دکارتی
معمولا از نمودار برای نشان دادن ارتباطی که بین دو کمیت استفاده میشود. در صنعت و تجارت از نمودارها برای گزارش تولید ماهانه و آمارهای فروش استفاده میشود. در جامعه شناسی از نمودارهای برای نشان دادن ارتباط بین میزان بیکاری و سطح سواد استفاده میشود و هزاران رابطه دیگر که در علوم مختلف توسط نمودارها با یکدیگر مقایسه میشوند. در واقع یک رابطه بین دو کمیت اغلب با معادله بیان میشود. برای نمایش این نمودارها در صفحه دکارتی با قرار دادن نقاط دلخواهی برای x یا y در معادله نمودار و یافتن جواب برای مولفه دیگر میتوانیم نقاط جواب معادله را شناسایی کرده و در صفحه مختصات آنها را پیدا کنیم و با رسم خط یا منحنی مربوطه نمودار معادله را رسم نماییم.
کاربردها
همان طور که در بالا توضیح داده شد یکی از کاربردهای صفحه دکارتی رسم نمودار ها و نمایش ارتباط بین کمیتهاست. یکی دیگر از کاربردهای مخصات دکارتی در بنای چرخ عظیمی است که امروزه چرخ و فلک نامیده میشود. چرخ فریس توسط جرج قریس (Veorge Ferris 1859 – 1896) آمریکایی که مهندس مکانیک بود طراحی شده است. اولین و بزرگترین در ۱۸۹۴ برای نمایشگاه جهانی کلمبیا در شیکاگو ساخته شد.




![[wpgmza id="1"]](https://hemmat.salamsch.org/hschool/wp-content/uploads/2020/12/location-marker-flat-80x80.png)