مقدمه
هندسه تحلیلی سه بعدی را ریاضیدانان قرن هفدهم از قبیل فرما ، دکارت و لاهیرا ابداع کردند، ولی دستگاه مختصاتی که امروزه بکار میبریم یوهان برنولی در نامهای به لا یب نیتس در ۱۷۱۵ صورت بندی کرد. در قرن هجدهم آلکسی کلرو (۱۷۱۳-۱۷۶۵). لئو نهارت اویکر (۱۷۰۷-۱۷۸۳) برجستهترین ریاضیدانانی بودند که هندسه سه بعدی را گسترش دادند به خصوص کلرو معلوم ساخت که یک رویه را میتوان با معادلهای بر حسب سه مختصه نشان داد و برای توصیف خمی در فضا به دوتا از این گونه معادلهها لازم است. او ایدههایش را در کتاب “تحقیق درباره خمهای با خمیدگی مضاعف” در ۱۷۳۱ مطرح کرد، وی در این کتاب معادلات چندین رویه درجه دوم از قبیل کره ، استوانه ، هذلولیوار و بیضیوار را آورد. توجه او در نهایت به شکل زمین بود که فکر میکرد نوعی بیضیوار باشد. گاسپار مونژهندسهدان پیشرو قرن هجدهم نیز مطالب زیادی درباره هندسه تحلیلی سه بعدی و دستگاههای مختصات مربوطه به آنها نوشته است.
 |
استوانه
رویهای که ترسیم آن و نوشتن معادلهاش از همه رویهها (البته با صرفنظر از صفحه) آسانتر است، استوانه میباشد. استوانه دویهای است از همه خطوطی که از یک خم واقع در صفحه میگذرند و با خط ثابتی موازیاند. در هندسه فضایی ، واژه “استوانه” را به معنی “استوانه مستدیر” به کار میبرند. هر خم f(x,y)=c واقع در صفحه xy استوانه ای را مشخص میکند که موازی محور z است. به همین نحو g(x,y)=c واقع در صفحه xz استوانهای را مشخص میکند که موازی محور y هاست و هر خم h(x,y)=c معرف استوانهای در صفحه yz است که موازی محور x است. خلاصه اینکه معادلهای بر حسب دو مختص از سه مختص دکارتی مشخص کننده استوانهای است که خطهای موازی با محور مختص سوم آن را میسازد.
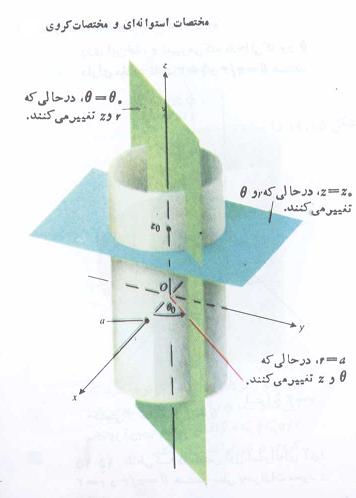
دستگاه مختصات استوانهای
ممکن است معادله یک رویه در یکی از دستگاههای سادهتر از معادله آن در دستگاه دکارتی باشد. در چنین مواردی استفاده از دستگاه نامناسب باعث صرفه جویی در وقت میشود. این موضوع در حل انتگرالهای چندگانه اهمیت بیشتری پیدا میکند. همان طور که میدانید حل برخی انتگرالهای سه گانه در دستگاه دکارتی گاها غیر ممکن میباشد، ولی با یک تغییر مختصات ساده به راحتی میتوانیم به جواب مورد نظر برسیم. در دستگاه مختصات استوانهای ، استوانههایی که محورشان در امتداد محور z هستند معادلات بسیار سادهای دارند. این دستگاه مختصات در فضا از طریق تلفیق مختصات قطبی در صفحه xy با محور z معمولی به دست میآید. به این ترتیب به هر نقطه در فضا یک یا چند سه تایی مختصات به صورت (r,θ,z) نسبت داده میشود. مقادیر x , y , r , θ در مختصات استوانهای با روابط معمولی زیر به هم مربوط اند:
x=r Sinθ و y=r Cosθ
Latex Error:
{r
۲+y^2}
و
Latex Error:
{tan \theta=\frac {y}{x}}
در واقع توسط روابط فوق میتوان یک نقطه در دستگاه مختصات دکارتی را به دستگاه مختصات استوانهای منتقل کرد. در مختصات استوانهای معادله r=a فقط دایرهای در صفحه xy را مشخص نمیکند بلکه استوانهای کامل حول محور z را توصیف میکند. خود محور z با معادله r=0 معین میشود. معادله θ=θ۰ توصیف کننده صفحهای است که شامل محور z است و زاویهای به اندازه θ۰ رادیان با قسمت مثبت محور x میسازد.
چند رابطه که مختصات دکارتی ، استوانهای و کروی را به هم مربوط میسازند.



![[wpgmza id="1"]](https://hemmat.salamsch.org/hschool/wp-content/uploads/2020/12/location-marker-flat-80x80.png)

