ماتریس مربعی

ماتریسی است که تعداد سطرها و ستونهای آن با هم برابر باشد.

ماتریس سطری

ماتریسی است که یک سطر دارد. مثلا

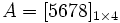
ماتریس ستونی

ماتریسی است که یک ستون دارد. مثلا

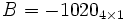
ماتریس 

ماتریسی است که فقط یک عضو دارد. مثلا

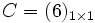
ماتریس صفر

تمام عضوهای آن ماتریس برابر صفر می‌باشد. این ماتریس در جمع ماتریسها حکم عدد صفر را در جمع اعداد حقیقی دارد یعنی عضو خنثی است.

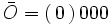
ماتریس واحد یا یکه

ماتریسی است مربعی که عضوهای قطر اصلی آن همگی برابر با یک و بقیه عضوهای آن برابر صفر می‌باشد. این ماتریس را با I نشان می‌دهند. مثلا

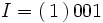
!ماتریس قرینه
اگر ماتریسی را در عدد ۱- ضرب کنیم قرینه آن ماتریس بدست می‌آید. بعبارت دیگر قرینه یک ماتریس ، ماتریسی است که عضوهای آن قرینه عضوهای ماتریس اصلی باشند.

ماتریس قطری

ماتریسی است مربعی که قطر اصلی آن اعداد حقیقی بوده و سایر عضوهای آن برابر صفر باشد. مثلا

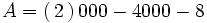
ماتریس عددی یا اسکالر

ماتریسی است قطری که عضوهای قطر اصلی آن برابر باشند. مثلا

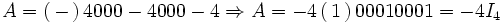
ماتریس منفرد

ماتریسی است مربعی که دترمینان آن برابر صفر باشد. یعنی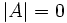 

ماتریس غیرمنفرد یا وارون‌پذیر

اگر در یک ماتریس مربعی دترمینان آن صفر نباشد به آن ماتریس غیرمنفرد می‌گویند. یعنی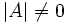 

ماتریس معکوس یا ماتریس وارون

ماتریس مربعی A را در نظر می‌گیریم اگر ماتریسی مانند B پیدا شود بطوریکه داشته باشیم AB=BA=I به ماتریس B وارون یا معکوس ماتریس A می‌گویند معمولا ماتریس معکوس A را بصورت 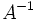 نشان می‌دهند و در نتیجه داریم:

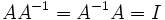
ماتریس همسازه

اگر در یک ماتریس مربعی به جای هر عضو ، کوفاکتور آن را قرار دهیم ماتریسی بدست می‌آید که به آن همسازه می‌گویند. ماتریس همسازه A را با N نمایش می‌دهند.

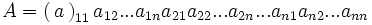
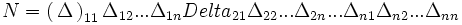
برای هر 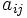 در ماتریس  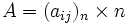، همسازه  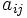برابر است با عدد
کوفاکتور عضو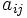  
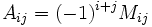
بطوریکه ، 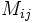 را دترمینان ماتریس حاصل از حذف سطر i ام و ستون j ام ماتریس A می‌توان تعریف کرد.

ماتریس وابسته یا الحاقی

به ترانسپوزه ماتریس همسازه A ماتریس وابسته A می‌گویند و آن را با 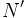 نشان می‌دهند.

ماتریس متقارن

اگر ترانسپوزه یک ماتریس با آن ماتریس برابر باشد آن ماتریس را متقارن می‌نامند بعبارت دیگر ماتریس A متقارن است در صورتیکه 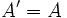 باشد. اگر در ماتریس جای سطرها و ستونها را عوض کنیم و ماتریس تغییر نکند به آن متقارن می‌گویند.

ماتریس ضدمتقارن یا آنتی‌متقارن

هرگاه قرینه ترانسپوزه ماتریس A برابر A شود، به آن ماتریس ضدمتقارن می‌گویند و داریم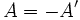 

ماتریس پایین مثلثی

اگر در یک ماتریس مربعی تمام عضوهای بالای قطر اصلی صفر باشند به آن ماتریس پایین مثلثی می‌گویند یعنی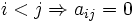 

ماتریس بالا مثلثی

اگر در یک ماتریس مربعی تمام عضوهای پایین قطر اصلی صفر باشند به آن ماتریس بالا مثلثی می‌گویند. یعنی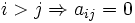

ماتریس متعامد

اگر در ماتریس مربعی A داشته باشیم 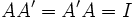به ماتریس متعامد می‌گویند.